6 Base Rates and Reference Classes
Let’s start by considering the following question:
What is the probability that Joe Biden is President of the United States on Nov. 1st, 2024?
[Note: This was written on Nov. 3rd, 2021.]
To answer this question, one strategy I would use is to look at base rates: the rate of occurrence of similar events. For instance:
What fraction of presidential terms are fully completed (last all 4 years)? The answer to this is 49 out of the 58 total terms, or around 84%.
On the other hand, we know that Biden has already made it through 288 days of his term. If we remove the 5 presidents who left office before that, there are 49 out of 53 or around 92%.
But alternately, Joe Biden is pretty old (78 to be exact). If we look up death rate per year in actuarial tables, it’s around 5.1% per year, so this leaves him with a ~15% chance of death or a 85% chance of surviving his term.
These are all examples of using base rates.
Base rates can be powerful as they allow us to draw analogies with related cases even when we don’t have directly relevant data or a trend line to extrapolate. In that sense they are like zeroth-order forecasting, but can work even when you don’t have a clear time series or other trend to base a forecast on.
6.1 Decomposing the Problem
We can take base rates one step further. If Biden doesn’t complete his term, the main reasons I can think of are:
- Death by natural causes
- Death by assassination
- Impeachment / resignation
- The presidency no longer exists (due to a coup, invasion, etc.)
So, we could estimate all of these using base rates, then add them up.
The last two are easiest: only one president has left office due to resignation (Nixon), so 1 out of 58 on impeachment / resignation. I’d put the presidency no longer existing at <1%, so together these add up to maybe 2%.
 [At the time of writing, PredictIt gave Biden a 22% chance of resigning before the end of his term. I feel confused about this.]
[At the time of writing, PredictIt gave Biden a 22% chance of resigning before the end of his term. I feel confused about this.]
Death by assassination: 4 out of 58 presidents, or around 7%. But only one of these was more than 288 days into the term, which would instead give 1.7%. I would subjectively put the probability a bit between these, at 3.5%.
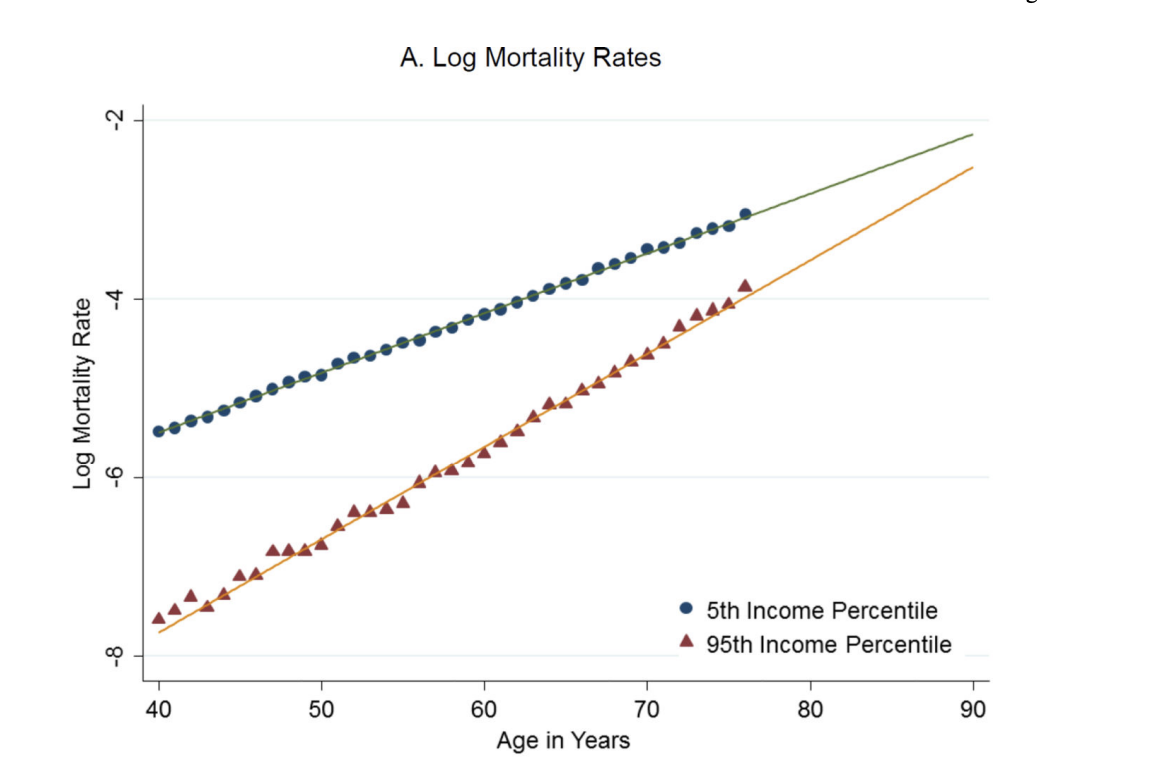
Death by natural causes: we previously gave this a 15% chance. But that’s neglecting that life expectancy increases with income, and Biden is pretty rich. Eyeballing the mortality curves here, I’m going to guess that this decreases his probability of death to around 70% of its baseline value 1. So we end up with 10.5% instead of 15%.
Adding these together gives 2 + 3.5 + 10.5 = 16%. So an 84% chance of completing his term.
What did we gain from applying this decomposition? The main thing is that it allows us to incorporate age when predicting death from natural causes, which feels correct to me. On the other hand, it left us with a very small sample size for assassinations, and in general left us to make a lot of arbitrary choices that might let personal biases creep in. That being said, the number is in the same ballpark but a bit lower than the 92% answer from the simplest method, which feels right given Biden’s age.
6.2 Other Examples
There are many cases where base rates are a useful tool. For instance, maybe I want to understand the probability that I get Covid in the next month (perhaps as a function of what activities I do).
Brainstorming exercise. What base rates would you use for the above question? What factors are most important to take into account?
Here are some other questions where base rates provide valuable information:
- What job will I have after I graduate Berkeley?
- How much Series A funding will this startup get?
- Will someone break Usain Bolt’s 100-meter dash 9.58s world record by the end of 2024?
- Will any new country join NATO in 2023?
Brainstorming exercise. What are other areas where base rates are helpful?
6.3 Dangers of Base Rates
As I hinted above, the flexibility of base rate forecasting also carries risk. If we make too many arbitrary choices when defining a base rate, we can succumb to our own cognitive biases. For instance, consider the following article that gave Trump a 3% chance of winning the 2016 election. Its reasoning invokes base rates, defining a reference class of “Candidates that are good with the media and give them something to write about but, let’s be real, could never be president”. They said Trump was in this reference class and no such candidate had ever won, so their base rate was 0%. (They then adjusted it up to 3% based on Trump’s strong polling performance.) If you find yourself doing something like this, watch out.
 Pro tip: Don’t do this.
Pro tip: Don’t do this.
The best ways to avoid failures like the Trump prediction are to look for the simplest reference classes you can find (only adjusting for obviously important and objective factors like age), or to average over lots of ways of constructing your reference class so that no single set of choices dominates the forecast.
6.4 Base Rates for Events That Haven’t Happened
What about base rates for events that have never happened? For instance, suppose that no U.S. president had ever resigned: should we really give a 0% probability of that happening to Biden? Probably not.
A rough rule of thumb is that if an event has had \(n\) opportunities to occur but has never happened, we assign probability \(\) to it happening the next time. So for instance, if someone is late to their first two meetings with me, I assign 25% probability to them being on time the next time.
To use this rule of thumb, we need to decide what \(n\) is. In the case of presidents resigning, \(n = 45\) seems pretty reasonable, but other situations can be more complicated. For instance, suppose we want to estimate the probability of military conflict between France and the United States in the next year. How far back should \(n\) go: e.g., should the Quasi-War influence our credence?
Here are some other examples where we care about events that haven’t happened yet:
- What is the probability of fully self-driving cars by 2030?
- What is the probability that we develop a cure for diabetes by 2025?
- What is the probability the FDA approves Paxlovid by Jan. 1st, 2022?
- What is the probability of California seceding from the U.S. by 2025?
Exercise. How would you choose \(n\) in the above cases? How reasonable does the \(n+2\) rule seem in each case? Are there any cases where an alternative prediction method seems better?
Generalization and alternatives. The \(n+2\) rule is a special case of Laplace’s rule of succession, which addresses a more general problem: if I repeat an experiment \(n\) times, and am successful in \(s\) of the \(n\) trials, what is the probability that I will be successful in trial \(n+1\)? Laplace’s rule provides the estimate \(\), which in the special case \(s = 0\) yields the \(\) recommendation above.
Laplace’s rule is formally derived by assuming that the events are i.i.d. and that their true probability \(p\) has a uniform prior, and then applying Bayes’ rule. The uniform prior can have strange implications: it implies that when \(n = 0\) (no observations so far), we should assign 50% probability to the event happening. For presidents resigning, this means assigning 50% probability to the first president resigning, which seems too high.
If you asked me to imagine the probability that George Washington would resign, I would’ve guessed something like \(= 0.25\). A simple generalization of the \(n+2\) rule to this case is to predict \(1 / [n + (1/\pi)]\). So for \(n = 45\) presidents I would give a \(\) probability of resigning, which is a bit smaller than the prediction from the \(n+2\) rule.
The above “\(n + (1/\pi)\)” rule can also be justified mathematically, using a different prior than the uniform distribution. We can often determine a good prior by appealing to some higher-level reference class. For a good example of this, I’d recommend looking at Tom Davidson’s report on semi-informative priors for AI development.
Brainstorming exercise. Suppose that instead of picking \(\) intuitively in the George Washington example, we wanted to set \(\pi\) using a base rate. What reference classes could we use?
In particular, this curve shows the log mortality rates for men in the 5th and 95th income percentiles in the US. At 76 years old, the mortality rate is around \(10^{-3}\) in the 5th percentile and \(10^{-4}\) in the 95th percentile. So we can approximate the median mortality rate (i.e. the baseline) as \(10^{-3.5}\). Since \((10^{-3.5} - 10^{-4}) / 10^{-3.5} \approx 70\%\), we deduce that the probability of death in the 95th percentile is around 70% of its baseline value.
 ↩︎
↩︎